how to find angle between two vectors

Angle between Two Vectors

The discussion on direction angles of vectors focused on finding the angle of a vector with respect to the positive x-axis. This discussion will focus on the angle between two vectors in standard position . A vector is said to be in standard position if its initial point is the origin (0, 0).

Figure 1 shows two vectors in standard position.

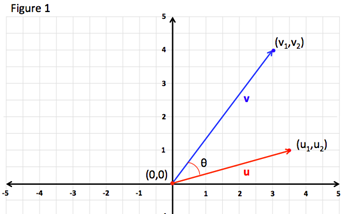
The angle between two vectors in standard position can be calculated as follows:

ANGLE BETWEEN TWO VECTORS:

If θ is the angle between two non-zero vectors in standard position u and v:

Where

0 \leq θ \leq 2 π

and

∥ v ∥ = \sqrt{v_{1}^{2} + v_{2}^{2}}

Let's look at some examples.

To work these examples requires the use of various vector rules. If you are not familiar with a rule go to the associated topic for a review.

Example 1: Find the angle θ between $u = 〈 6, 3 〉$ and $v = 〈 5, 13 〉$ .

Step 1: Find the dot product of the vectors.

Remember the result will be a scalar.

$u \cdot v = u_{1} v_{1} + u_{2} v_{2}$

$u \cdot v$

$(6 \cdot 5) + (3 \cdot 13)$

$30 + 39 = 69$

Step 2: Find the magnitudes of each vector.

$∥ v ∥ = \sqrt{v_{1}^{2} + v_{2}^{2}}$

||u|| = $\sqrt{u_{1}^{2} + u_{2}^{2}}$

||u|| = $\sqrt{6^{2} + 3^{2}}$

||u|| = $\sqrt{45} = 3 \sqrt{5}$

______________________________

||v|| = $\sqrt{v_{1}^{2} + v_{2}^{2}}$

||v|| = $\sqrt{5^{2} + 13^{2}}$

||v|| = $\sqrt{194}$

Step 3: Substitute and solve for θ.

$c o s θ = \frac{u \cdot v}{∥ u ∥ \cdot ∥ v ∥}$

$cos θ = \frac{69}{3 \sqrt{5} \cdot \sqrt{194}} = \frac{23}{\sqrt{970}}$

$θ = \cos^{- 1} \frac{23}{\sqrt{970}}$

$θ \approx 42 °$

Example 2: Find the angle θ between $u = 〈 3, - 6 〉$ and $v = 〈 8, 4 〉$ .

Step 1: Find the dot product of the vectors.

Remember the result will be a scalar.

$u \cdot v = u_{1} v_{1} + u_{2} v_{2}$

$u \cdot v$

$(3 \cdot 8) + (- 6 \cdot 4)$

$24 - 24 = 0$

Step 2: Find the magnitudes of each vector.

$∥ v ∥ = \sqrt{v_{1}^{2} + v_{2}^{2}}$

||u|| = $\sqrt{u_{1}^{2} + u_{2}^{2}}$

||u|| = $\sqrt{3^{2} + {(- 6)}^{2}}$

||u|| = $\sqrt{45} = 3 \sqrt{5}$

______________________________

||v|| = $\sqrt{v_{1}^{2} + v_{2}^{2}}$

||v|| = $\sqrt{8^{2} + 4^{2}}$

||v|| = $\sqrt{80} = 2 \sqrt{20}$

Step 3: Substitute and solve for θ.

$c o s θ = \frac{u \cdot v}{∥ u ∥ \cdot ∥ v ∥}$

As soon as you determine that the dot product is 0 you do not need to calculate the magnitudes. They are completed here for your benefit.

Note that when two vectors in standard position have a dot product of 0 the angle between them is 90°.

$c o s θ = \frac{u \cdot v}{∥ u ∥ \cdot ∥ v ∥}$

$cos θ = \frac{0}{3 \sqrt{5} \cdot 2 \sqrt{20}} = \frac{0}{6 \sqrt{100}} = \frac{0}{60}$

$θ = \cos^{- 1} 0$

$θ = 90 °$